二叉树是树结构的一种,一种一对多的逻辑关系,
基本概念:父节点有且最多只有两个子节点
树的名词解释:
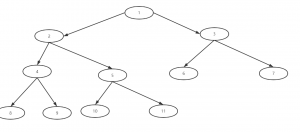
根节点:二叉树的顶层节点有且只有一个,如图中的1节点
父节点:相比较的概念的,如:2是5和4的父节点,1是2的父节点
子节点:和父节点一样也相对的 如:对于8和9而言它是4的子节点,而对于4它是2的子节点……
层:它来判断树的高度,如图中有4层
权:指每个节点的存储的值(数据),图中每个节点存储了数字这就是权
路径:指从当前节点到其他节点的路线,如:从2到5的路线就是路线,每个节点都有一个左右指向
叶子节点:没有子节点的节点,如:8,9,10,11,6,7都是叶子节点
子树:类比于一颗大树的树枝,如:2,4,5就叫一颗子树
树的高度:最大层数
------满二叉树和完全二叉树-------
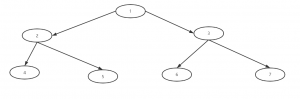
满二叉树:所有的叶子节点都在最后一层,节点的总数=2^n-1(n为层数)
图中就是一个满二叉树,所有节点都在最后一层,它的节点总数=2^3-1为7个节点
完全二叉树:所有的叶子节点都在最后一层或者倒数第二层,最后一层向左连续,倒数第二层向右连续
假如5,6,7其中一个没有就不存在连续也就不完全二叉树
--------二叉树的实现-----------
在数据结构的分类中物理存储分两类:顺序存储和链式存储
在数据结构中每一个逻辑结构都依赖于物理存储结构,通过物理结构来实现逻辑结构
二叉数有两种实现方式,一种是链式存储二叉树,一个顺序存储二叉树(堆的实现依赖于顺序二叉树)
------------链式二叉树-------------
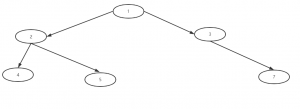
构建图中的二叉树:
public class chaintree {
public static void main(String[] args) {
//建立节点:定义6个节点
predata a=new predata(1);
predata b=new predata(2);
predata c=new predata(3);
predata d=new predata(4);
predata e=new predata(5);
predata f=new predata(6);
//给他们建立关系
//a点的左节点是b,a的右节点是c
a.setLife(b);
a.setRight(c);
//b的左节点是d,右节点是e
b.setLife(d);
b.setRight(e);
//c的右节点是f,没有左节点
c.setRight(f);
//将节点关系放进树里面
tree wql=new tree(a);
wql.front();//1,2,4,5,3,6
}
}
//定义树把节点类的节点联系放进树
class tree{
private predata treewql;
public tree(predata treewql){
this.treewql=treewql;
}
//从树类中调用遍历方法
//前序遍历
public void front(){
if(treewql==null){
System.out.println("树为空");
}else{
treewql.front();
}
}
//中序遍历
public void centre(){
if(treewql==null){
System.out.println("树为空");
}else{
treewql.centre();
}
}
//后序遍历
public void later(){
if(treewql==null){
System.out.println("树为空");
}else{
treewql.later();
}
}
}
//节点类
class predata{
private predata life;//定义左子节点
private predata right;//定义右子节点
private int val;//给我树一个权值
//初始化值
public predata(int val){
this.val=val;
}
//给当前节点设置它的左节点
public void setLife(predata life) {
this.life = life;
}
//给当前节点设置它左节点
public void setRight(predata right) {
this.right = right;
}
//toString方法
@Override
public String toString() {
return "predata{" +
"val=" + val +
'}';
}
//前序遍历:先输出父节点,再输出左子节点,最后是右子节点
public void front(){
System.out.println(this);//前序遍历首先输当前节点也就是父节点
if(this.life!=null){//输出左子节点,先判断左子节点是否为空,再递归输出左子节点
this.life.front();
}
if(this.right!=null){//输出右子节点,先判断右子节点是否为空,再递归输出右子节点
this.right.front();
}
}
//中序遍历:先输出左子节点,再输出父节,最后是右子节点
public void centre(){
//中序遍历首先输当前节点也就是父节点
if(this.life!=null){//输出左子节点,先判断左子节点是否为空,再递归输出左子节点
this.life.centre();
}
//中间输出父节点
System.out.println(this);
if(this.right!=null){//输出右子节点,先判断右子节点是否为空,再递归输出右子节点
this.right.centre();
}
}
//后序遍历:先输出左子节点,再输出右子节点,最后是父节点
public void later(){
//中序遍历首先输当前节点也就是父节点
if(this.life!=null){//输出左子节点,先判断左子节点是否为空,再递归输出左子节点
this.life.later();
}
//中间输出右子节点
if(this.right!=null){//输出右子节点,先判断右子节点是否为空,再递归输出右子节点
this.right.later();
}
//最后输出父节点
System.out.println(this);
}
}
前序遍历,中序遍历,后序遍历的区别在于父节点输出的位置,前序就是父节最先输出,以此类推
前序:父节点 -> 左子节点 -> 右子节点
中序:左子节点 ->父节点 -> 右子节点
后序:左子节点 ->右子节点 -> 父节点
----------顺序存储二叉树---------
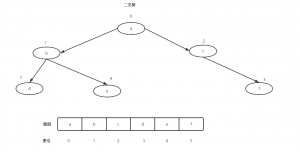
顺序存储二叉树与链式存储二叉树不同,它的节点是数组的一个个区间,数组中存储的值就是树的权
树的左节点=2*当前节点在数组中的索引+1
树的右节点=2*当前节点在数组中的索引+2
通过索引来计算左右树
如图中:
a的左节点=2*0+1(索引)
c的右节点=2*2+2(索引)
public class ordertree {
public static void main(String[] args) {
int[] WQL=new int[]{1,2,3,4,5,6};
datawql a=new datawql(WQL);
a.alter1(0); //1,2,4,5,3,6
}
}
class datawql{
int[] datas;
public datawql(int[] datas){
this.datas=datas;
}
//前序遍历
public void front1(int index){//给出要遍历的起始节点的索引
if(datas[index]!=0 && index<datas.length) {
System.out.println(datas[index]);
}
if((index*2+1)<datas.length){
front1(index*2+1);
}
if((index*2+2)<datas.length){
front1(index*2+2);
}
}
//中序遍历
public void concre1(int index){//给出要遍历的起始节点的索引
if((index*2+1)<datas.length){
concre1(index*2+1);
}
if(datas[index]!=0 && index<datas.length) {
System.out.println(datas[index]);
}
if((index*2+2)<datas.length){
concre1(index*2+2);
} }
//中序遍历
public void alter1(int index){//给出要遍历的起始节点的索引
if((index*2+1)<datas.length){//index大于数组长度就声明不存在
alter1(index*2+1);
}
if(datas[index]!=0 && index<datas.length) {
System.out.println(datas[index]);
}
if((index*2+2)<datas.length){
alter1(index*2+2);
} }
}
-----------堆排序-----------
堆排序是利用堆这个数据结构而设计的一种排序算法(是一种不稳定排序)
堆是一个完全二叉树它有两个特性:
大顶堆:父节点比子节点大(不比较叶子节点的大小)
小定堆:父节点比子节点小(不比较叶子节点的大小)
public class heapsort {
public static void main(String[] args) {
int[] a=new int[]{2,3,1,6,4};
heap1 s=new heap1(a);
}
}
//将堆进行排序
class hea1sort{
heap1 c;
public hea1sort(heap1 c){
this.c=c;
}
public void sort(){
for(int a=c.a.length/2-1;a>=0;a--){
c.adjustheap(a);
}
}
}
//定义一个堆
class heap1{
int[] a;
public heap1(int[] a){
this.a=a;
}
//将数组的二叉树转化成一个堆
public void adjustheap(int i){//非叶子节点的索引
int[] n=a;
int temp=n[i];//保存当前节点的值
for(int i1=i*2+1; i1>=0; i1=i*2+1){
//接收当前节点得到左节点(i*2+1),判断左节点是否比右节点大,如果比右节点小就把左节点的索引改成右索引
if(i1+1<n.length && n[i1+1] >n[i1]){
i1++;
}
//判断当前非叶子节点的根节点是是否比子节点大,如果小就把子节点的值赋给当前节点也就是a[i]
if(i1+1<n.length && n[i] < n[i1]){
n[i]=n[i1];
i=i1;//把i(当前的父节点索引)换成子节点索引
}else {
break;//这个方法只判断一个非叶子节点
}
n[i]=temp;//如果前后的if条件符号就把之前父节点的值再给子节点
}
}
}






Comments | NOTHING